VerilogA Day 03: The Anatomy of a Verilog-A Module

Posted on: October 26, 2024

Understanding the Structure of a Module

A Verilog-A module typically includes several key elements:

• Library Includes: Always start by including the necessary libraries to access fundamental constants and disciplines.
• Module Declaration: This is where you define the module name and its ports.
• Parameter Declaration: Use parameters to customize your model, just like adjusting the size of a wrench to fit different nuts and bolts.
• Analog Block: Here’s where the magic happens! You define the behavior of your module, similar to how you would decide which tool to use for a task.

Step 1: Crafting a Verilog-A Model for an RC Circuit

Let’s take our resistor knowledge and add a new ingredient: a capacitor. When you connect these two in series, you get an RC circuit that’s fantastic for smoothing signals. Here’s how it looks in code:

`include "disciplines.vams" // Include fundamental constants
`include "constants.vams"   // Include Verilog-A libraries
module rc_circuit(p, n);        // Declare module with two ports 'p' and 'n'
  inout p, n;                   // Define 'p' and 'n' as analog ports
  electrical p, n, mid;         // Declare nodes 'p', 'n', and 'mid' as electrical

  parameter real R = 1k;        // Set resistance (1k ohm by default)
  parameter real C = 1n;        // Set capacitance (1 nF by default)

  analog begin
    I(p, mid) <+ V(p, mid) / R; // Current through resistor (I = V / R)
    I(mid, n) <+ ddt(C * V(mid, n)); // Current through capacitor (I = C * dV/dt)
  end
endmodule
    

This model builds a basic RC circuit. The resistor’s behavior is governed by Ohm’s law (current = voltage / resistance), while the capacitor’s behavior is a little more dynamic, responding to the change in voltage over time. It’s like a sponge filling up with water at a rate determined by the input current.

Step 2: Simulating the RC Circuit in Virtuoso’s ADE Explorer

Ready to bring it to life? Fire up ADE Explorer in Cadence Virtuoso:

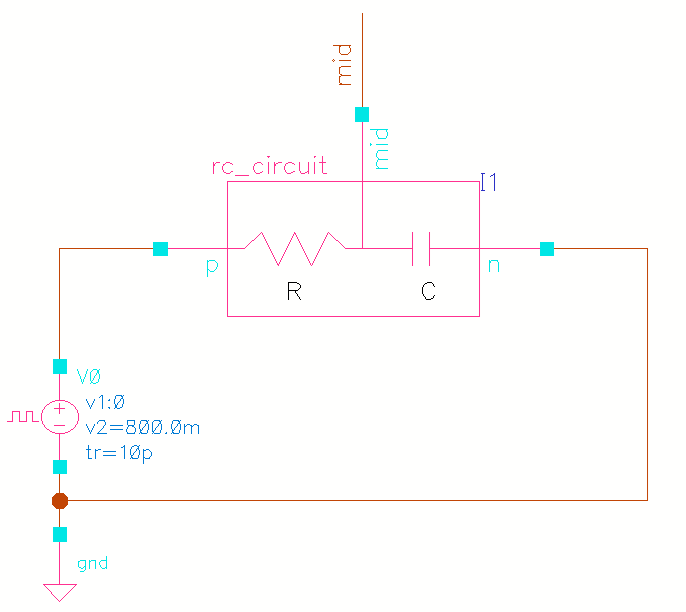
1. Create a new cell for rc_circuit and paste in your Verilog-A code.
2. Design a schematic with a "pulse voltage source" connected to p and ground on n. The circuit should look like this!

3. Open ADE Explorer and set up a transient analysis to observe the capacitor charging and discharging over time. Here is the maestro view from ADE Explorer.

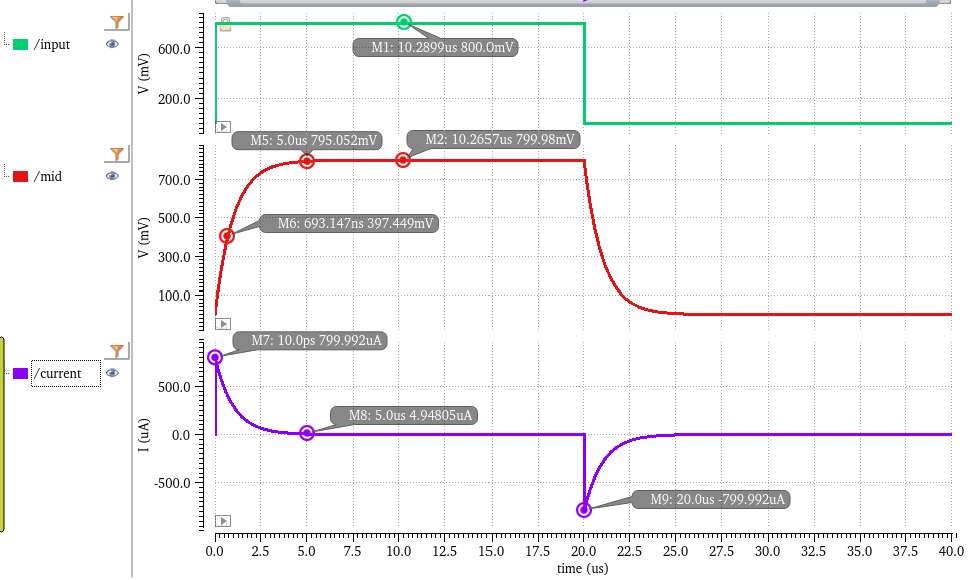
4. Plot the voltage across the capacitor and the circuit current in Virtuoso Visualization & Analysis XL. After running the simulation, you should see the plots for capacitor voltage and current just as expected. With a resistance of 1 KΩ and a capacitance of 1 nF, the output voltage should nearly reach the supply voltage (VDD) after 5τ (time constants). As shown in the graph, by 5 µs, the capacitor voltage is almost at VDD. Interestingly, the capacitor voltage hits half of VDD at 0.693τ! (Fun fact: I once faced an interview question about when the capacitor voltage reaches half of VDD, and I blanked out! Unsurprisingly, I wasn’t selected. But hey, failure teaches you valuable lessons, right?)

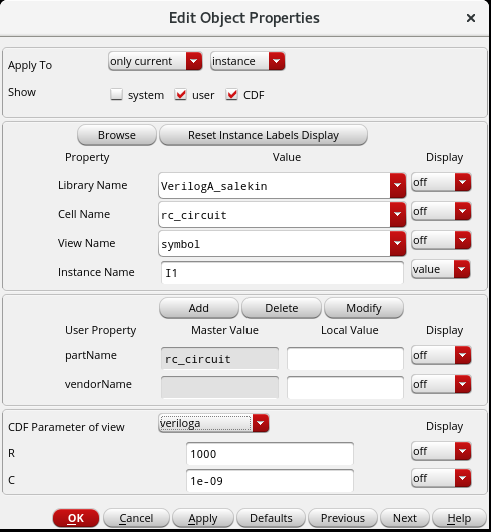
5. I can already hear the question brewing in your mind: 'How can I tweak the values of my RC network here?' Great question! All you need to do is hit q on the rc_circuit schematic and choose CDF Parameter of View as veriloga. Voilà! Now you can change the values of R and C to your heart's content. And do you know why these options are available? Oh, I know you guessed it! It’s because, while crafting your Verilog-A code, you cleverly used the parameter keywords for R and C, setting default values of 1k and 1n respectively. This is how it all comes together in Virtuoso!

6. And finally, I changed the value of the Resistor to 2 KΩ. As expected, with the increased time constant, the capacitor voltage will take more time to reach to VDD. Check out the below plots to satisfy your insatiable mind 😉

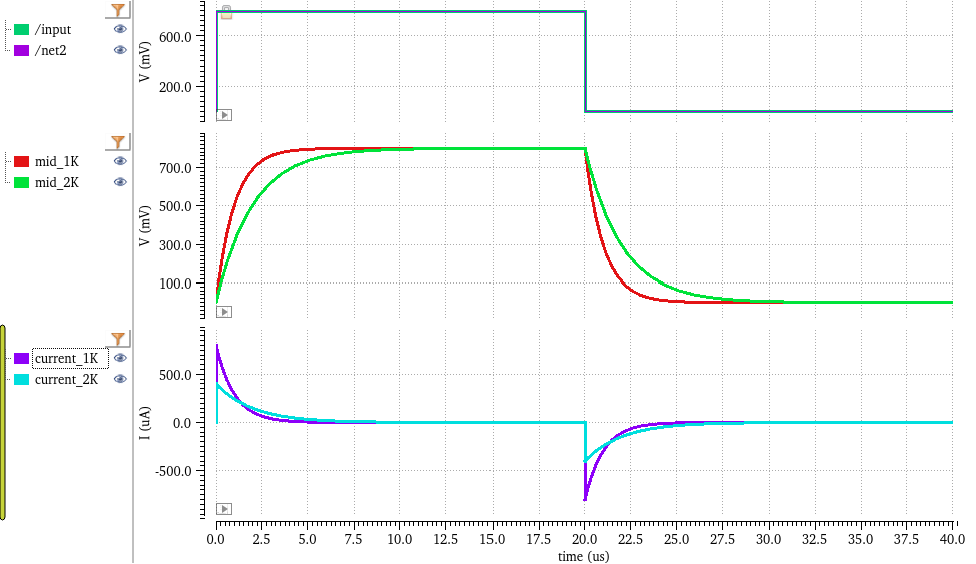
Watching the capacitor voltage rise and settle feels like observing a wave calm after the initial energy burst—a real-life view of electrical behavior.

Step 3: Understanding the 'Guts' of the Circuit

The 'guts' (core parts) here include the resistor and capacitor, each controlled by parameters R and C. We use Verilog-A's ddt() function to model the capacitor, where ddt() represents the derivative over time. Picture it as capturing the steepness of a hill as you go up or down; here, it measures how the capacitor’s voltage changes.

Wrap-Up

In Day 3, you’ve taken a closer look at how Verilog-A modules are structured and gained hands-on experience simulating a real circuit. Tomorrow, in Day 4, we’ll dive into understanding ports and electrical nodes in Verilog-A to get even closer to how these circuits connect and work together. Excited? Stay tuned!